Fold and Traverse

Introduction

Folding is the act of reducing a structure to a single value.

We can see them as consumers or comonads.^[1]

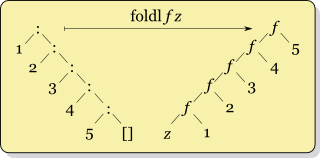
foldl/foldr

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f v [] = v
foldr f v (x:xs) = f x (foldr f v xs)

foldl :: (s -> a -> s) -> s -> [a] -> s
foldl  f v []     =  v
foldl  f v (x:xs) =  foldl f (f v x) xs

Both functions take 3 arguments: - a combining function 'f' - a default value 'v' - the data to be folded.

The default value 'v' deals with the empty element of the list []. For non empty list, foldl1/foldr1 is best suited.

foldr

You can think of foldr non-recursively as simultaneously replacing each (:) in a list by a given function, and [] by a given value:

foldr (-) 0 (1:2:3:[]) = (1 - ( 2 - (3 - 0))) = (1 - (2 - 3) = (1 - ( -1 ) = 2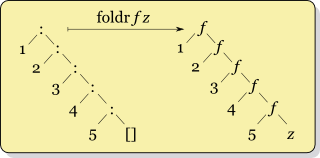

Foldr is handy if f is not strict in both arguments. That way we can rely on laziness to stop the recursion (or build an infinite list). Map for instance has to use foldr to maintain its laziness capabilities:

map = foldr (\x ys -> f x : ys) []
-- or map' = foldr ((:) . f) []

-- of course it can also be defined with recursion only
map' :: (a -> b) -> [a] -> [b]
map' _ [] = []
map' f (x:xs) = f x : (map f xs)

-- ex
takeWhile (< 12) $ map (*2) [1..]

foldl

On the other hand, when the whole list needs to be traversed (sum or reverse are two examples), foldl' is actually more efficient in term of memory space.

foldl (-) 0 (1:2:3:[]) = (0 - 1) - 2 - 3 = -6

reverse = foldl' (flip (:)) []

The strict version List.foldl' should always be used instead of the foldl from Prelude. The Foldable type class comes with foldl defined strictly.

Foldl package

To get a better representation for fold we need to transform the function into data.

{-# LANGUAGE ExistentialQuantification #-}
-- existential datatype (note that `x` does not appear on the left side)
data Fold a b
--                    step func      initial acc     extract func (done)
 = forall x . Fold  (x -> a -> x)       x             (x -> b)

-- expressed as a GADT it would be:
data Fold a b where
  Fold :: (r -> b) -> (r -> a -> r) -> r -> Fold a b

Fold is a functor, a monoid and an applicative. It is also a profunctor and a comonad. It is actually isomorphic to a Moore machine (see https://www.fpcomplete.com/school/to-infinity-and-beyond/pick-of-the-week/part-2)

-- | Apply a strict left 'Fold' to a 'Foldable' container
fold :: Foldable f => Fold a b -> f a -> b
fold (Fold step begin done) as = F.foldr cons done as begin
  where
    cons a k x = k $! step x a

This makes it possible to define cleanly the function average without traversing twice the foldable container.

average = (/) <$> sum <*> genericLength

sum :: Num a => Fold a a
sum = Fold (+) 0 id

genericLength :: Num b => Fold a b
genericLength = Fold (\n _ -> n + 1) 0 id

λ> fold average [1..10000000]

Fold is also a profunctor and a comonad.

Alternative monoid definition

As explained in Gabriel’s beautiful fold talk, Fold can similarly be defined as

data Fold i o = forall m . Monoid m => Fold (i -> m) (m -> o)

This approach can express parallel computation but it won’t encode stateful folds.

FoldM

data FoldM m a b =
  -- | @FoldM @ @ step @ @ initial @ @ extract@
  forall x . FoldM (x -> a -> m x) (m x) (x -> m b)

Fold is equivalent to FoldM Identity. You use generalize (with no performance penalty) to get a FoldM from a Fold:

generalize :: Monad m => Fold a b -> FoldM m a b

In the turtle library, FoldM plays the role of a consumer and Shell the role of a Producer. fold is how you connect them together.

Foldable/Traversable

Fold: fold from the foldl take as an argument any Foldable structure. Foldable are structures that we can reduce into a single result.

class Foldable t where
  fold    :: Monoid m => t m -> m
  foldMap :: Monoid m => (a -> m) -> t a -> m
  foldMap g = mconcat . map g

λ> foldMap Sum [1,2,3,4]
Sum {getSum = 10}

fold and foldMap require the elements of the Foldable to be monoids.

In Data.Foldable, mapM is defined with foldr (which is kind of mind blowing)

mapM_ :: (Foldable t, Monad m) => (a -> m b) -> t a -> m ()
mapM_ f = foldr ((>>) . f) (return ())

Traversable: When you traverse a structure you actually want to keep it intact. The function traverse is exactly mapM generalized for all Foldable`s. Traversable applies any applicative effect; traverse is an "effectful" fmap.

class (Functor t, Foldable t) => Traversable t where
  traverse  :: Applicative f => (a -> f b) -> t a -> f (t b)
  traverse f = sequenceA . fmap f
  mapM = traverse
  sequenceA :: Applicative f => t (f a) -> f (t a)
  sequenceA = traverse id

for = flip traverse

1. Unfolding is then associated to producers or monads.